Follow-up:
After looking back at the previous post I did notice one mistake. The shape for the following diagram should have been 1 2 3 instead of 2 3. If the shape had been 2 3 then the diagram would have had a plane rather than a cube as the ‘shape structure’.
1 2 3 $ 0
Augmenting Frank’s Dual-View Representation by Simplifying:
After several weeks of reflection, I realized that the previous solution to visualizing Frank’s Dual-View could be made simpler by displaying the absence of edges when there are zero valued dimensions in the shape. The following post will compare the two options with a following critique of the differences.
Case 0 – Empty shape for scalar value – Shape ’empty’
Old version

New version

Critique: The only difference here is colour to distinguish the two approaches as we move forward. Remember that scalar values in J do not have a shape of 0, but instead have a shape that is an empty list. Since there is no 0 in an empty list there is no change in representation of scalars.
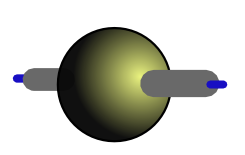
Case 1 – A list of zero items – Shape 0
Old version
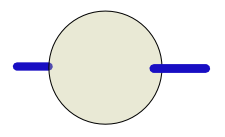
New version
Critique: Both versions have the axle indicating that this is a list and that items can be added. Both versions are also greyed out as a visual cue that this is an empty list. The new version shows that the dimension that is zero is along the x axis (the only axis, as indicated by the axle) and so this is an empty list, as opposed to an empty matrix or cube which we will see later. Even though this adds an element in the visualization of an empty array, it will provide a more simple representation of non-empty arrays.
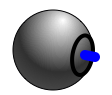
Case 2 – A list of one item – Shape 1
Old version
New version

Critique: This is where the advantage of the new approach starts to appear. Instead of the extra horizontal line, only the line presenting the one dimensional shape is included. The colour indicates that the shape is non-zero immediately.
Case 3 – A matrix of one item – Shape 1 1
Old version

New version
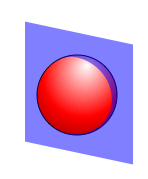
Critique: The advantage continues as the plane immediately indicates the two dimensional shape and the single sphere indicates only one item. No extra lines required for the vast majority of arrays which are non-empty.
Case 4 – A cube of one item – Shape 1 1 1
Old version
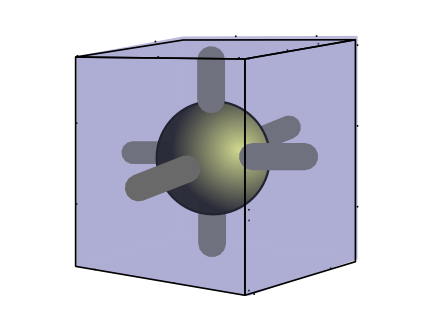
New version
 Critique: Again we have a single atom and the surrounding cube indicates three dimensions. The extra edges in the previous version are not required which really cleans up the display
Critique: Again we have a single atom and the surrounding cube indicates three dimensions. The extra edges in the previous version are not required which really cleans up the display
Case 5 – A matrix of one item – Shape 0, Shape 0 1, and Shape 1, 0
Shape 0

Shape 0 1

Shape 1 0

Critique: The displays of these three empty arrays show that the one dimensional and two dimensional are clearly distinguishable, as is the difference between Shape 0 1 and Shape 1 0 matrices.
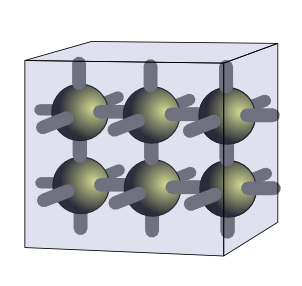
Case 6 – A cube of shape 1 2 3
Old version

New version

Critique: The spacing of the spheres easily shows the shape of the array and the enclosing cube outline immediately shows that the array has a three dimensional shape. If it were two dimensions the spheres would be embedded in a two dimensional plane. Again no more and no less than what is required to differentiate and describe the shape.
Case 7 – A cube of shape 0 2 3

Critique: This one was thrown in to show how a zero value in the leading axis of a three dimensional array would look. There are two rows and three columns of zero items which is why the spheres are greyed out with a front facing zero mark on the z axis. Contrast this with the 1 2 3 shape described in the preceding example.
Case 8 – A cube of shape 2 2 3
Old version

New version

Critique: I think that I may want to play around with the spacing on this one as this is one case where the new representation actually seems more confusing than the old version. Part of it may be the inherent structure that the extra edges provide, but I think this can be made up by using the spacing to reveal the relationships between the spheres as rows and columns. The text version of J uses this spacing to great effect, so I feel I am moving the right direction even though this version feels relatively unorganized.
In closing:
This time I promise; the next post will look at the representation of higher ranked arrays. I was happy to spend the extra time revising the display, as the higher dimensional representations really benefit from the cleaner look. Until next time, I look forward to any feedback you may have.
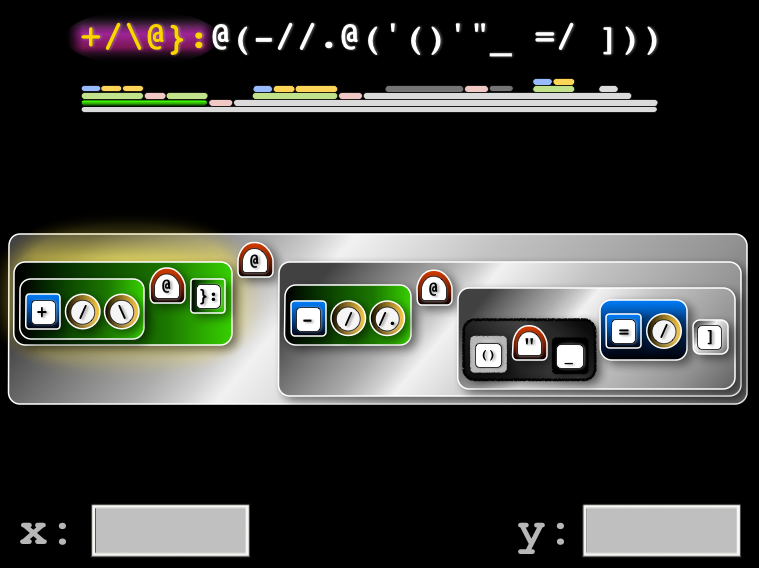 Previous visual display of ambivalent verb in Jig
Previous visual display of ambivalent verb in Jig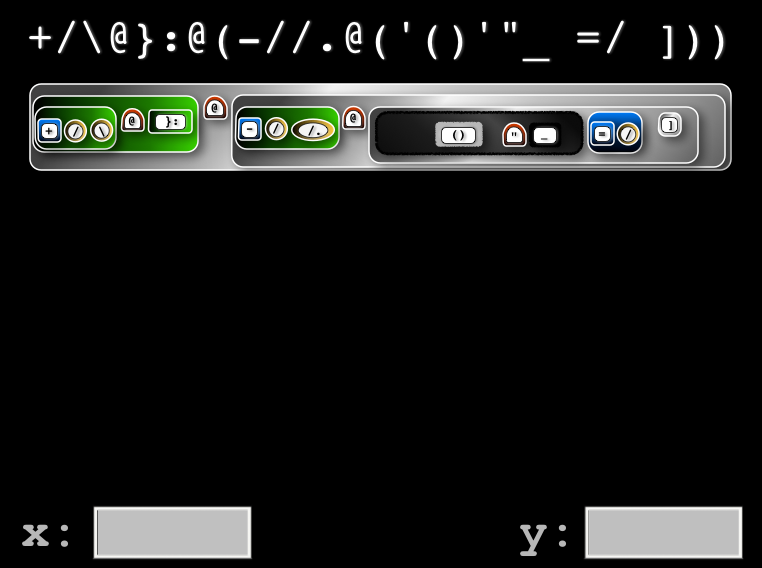 New visual display of ambivalent verb in Jig
New visual display of ambivalent verb in Jig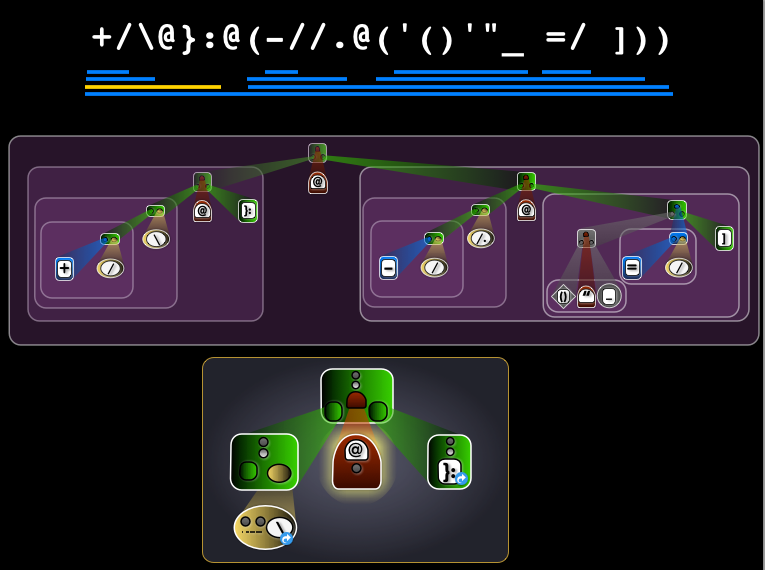
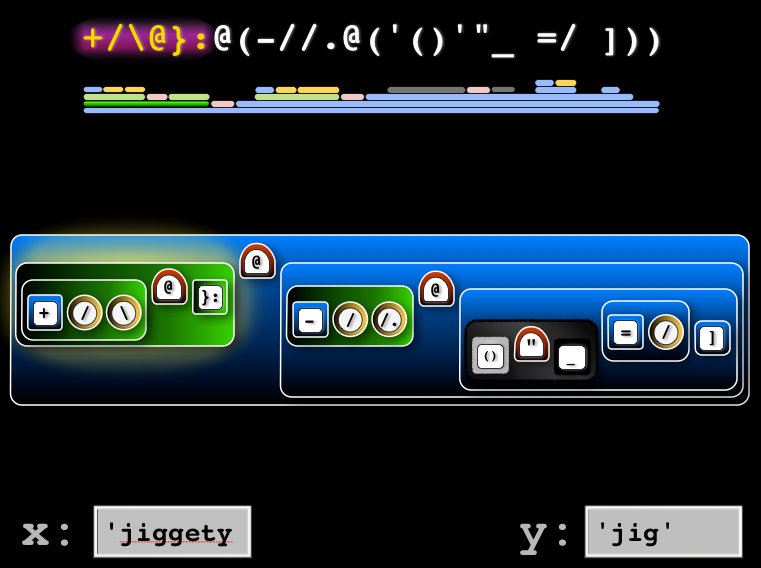
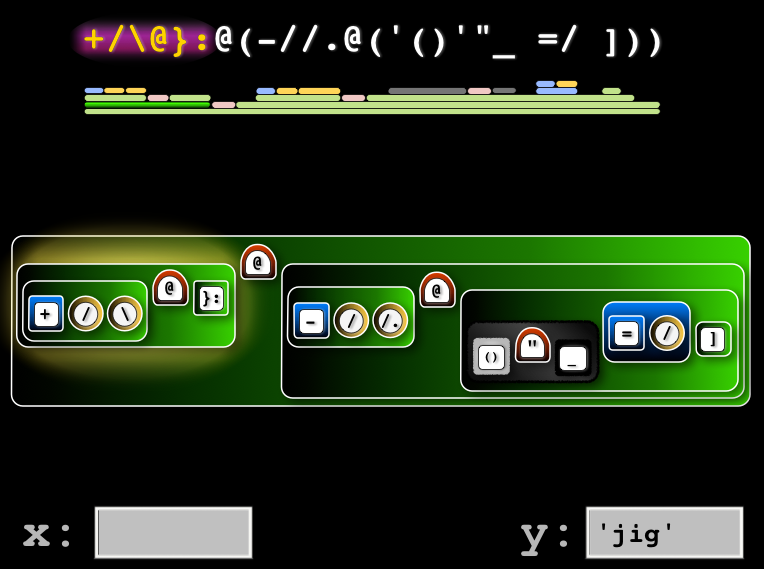

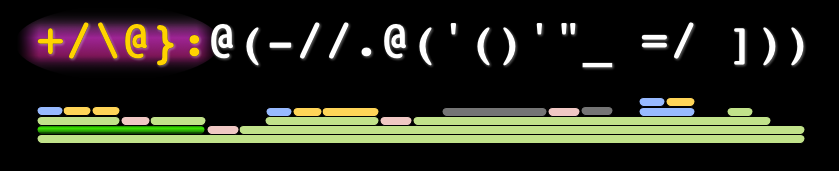
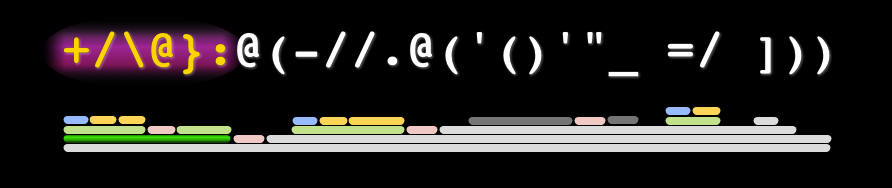
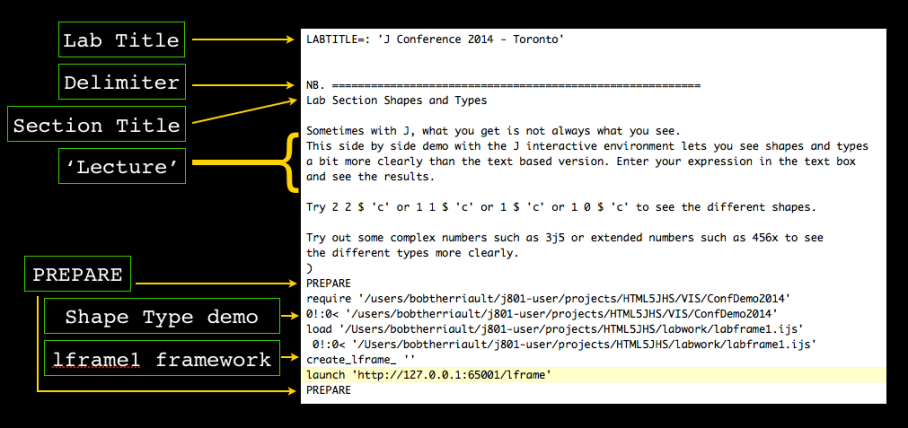
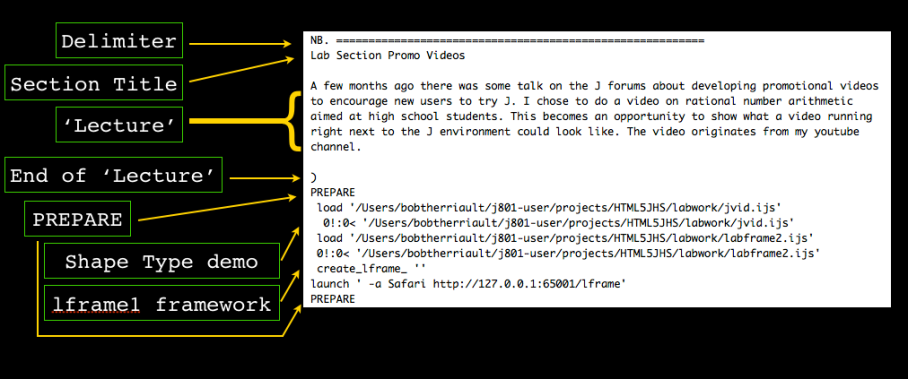
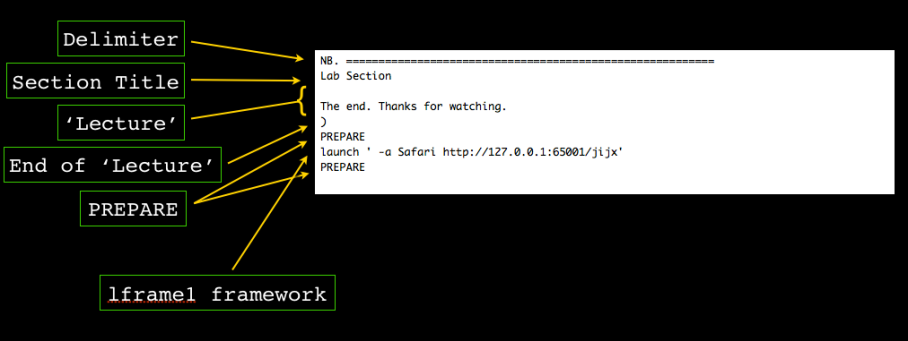 The final lesson returns back to the interactive jhs environment.
The final lesson returns back to the interactive jhs environment.

















You must be logged in to post a comment.