Follow Up:
My previous post included a verb to facilitate visualization of the Dual-View representation by returning coefficients representing array components:
arrayCoeff =: +//.@(*/)/@,.&1
Unfortunately, this verb fails for scalars because it can’t deal with the empty list shape of rank 0 arrays.
arrayCoeff '' |domain error: arrayCoeff | arrayCoeff ''
A better solution has the array itself as the argument, then determines its shape and triggers an exception when dealing with scalars.
arrayCoeffS =: +//.@(*/)/@,.&1`1:@.(''&-:)@$
where
(''&-: )@$
returns 1 for a scalar argument.
arrayCoeffS 4 NB. Scalar, array rank 0, shape '' 1 arrayCoeffS 3 $ 4 NB. Vector, array rank 1, shape 3 3 1 arrayCoeffS 2 3 $ 4 NB. Matrix, array rank 2, shape 2 3 6 5 1
Augmenting Frank’s Dual-View Representation:
This will allow arrays of shape 0 and shape 0 1 to be shown as distinct.
The Dual-View shows these shapes as identical because rank 2 can’t be represented by a single edge.
arrayCoeffS 0$0 NB. Empty list of rank 1 0 1arrayCoeffS 0 1$0 NB. No list of length 1 (rank 2) 0 1 1
Clearly they differ in the rank 2 array’s planar component, and changing the orientation of the single edge to indicate the plane is identical to the result of:
arrayCoeffS 1 0$0 NB. One list of length 0 (rank 2) 0 1 1
The way forward is to display the rank of the array even when the zero valued axes are not present. With distinguishable ranks, rank 1 and 2 arrays will be distinct. For rank 0 (scalar), the representation is the disk alone.
arrayCoeffS 2 NB. Scalar value of 2 (rank 0) 1
Arrays of rank 1 have a horizontal line through the disk indicating that the list can add items either before or after the value. If the shape is 0, only this rank line is shown with an empty value – a greyed out disk.
A non-zero axis uses thicker edges with rank line extended.
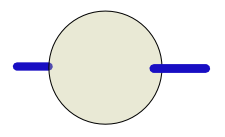
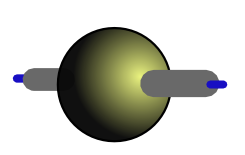
Rank 2 arrays indicate rank as an x-y plane encompassing the disk, allowing axes indication without affecting rank representation.
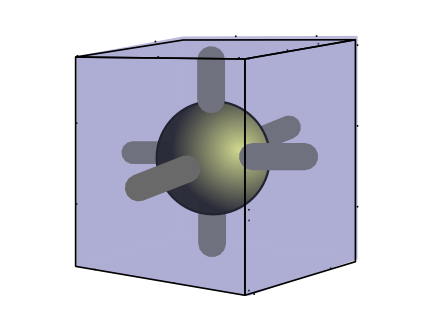
With rank 3 the embedding structure is a cube, with potential axes in three dimensions.
By including the rank information the augmented Dual-View shows previously indistinguishable arrays distinctly:
0$0
0 1 $ 0
1 0 $ 0
While typical arrays display as expected.
2 3 $ 0
2 2 3 $ 0
In the next post I will look at the representation of higher ranked arrays. Until then, I look forward to any feedback you may have.
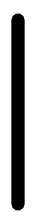






















You must be logged in to post a comment.